В4 Начала теории вероятностей

Конспект к уроку "Начала теорий вероятностей" 

Задания по теории вероятности делятся всего на 2 типа:

Классическое определение вероятности

Теоремы о вероятностях событий

Вероятность — это числовая характеристика возможности наступления какого-либо события. Вероятностью события А называется отношение числа m случаев, благоприятствующих его наступлению, к числу n всех возможных случаев

Обозначение: Р А=mn

Классическое определение  вероятности : 

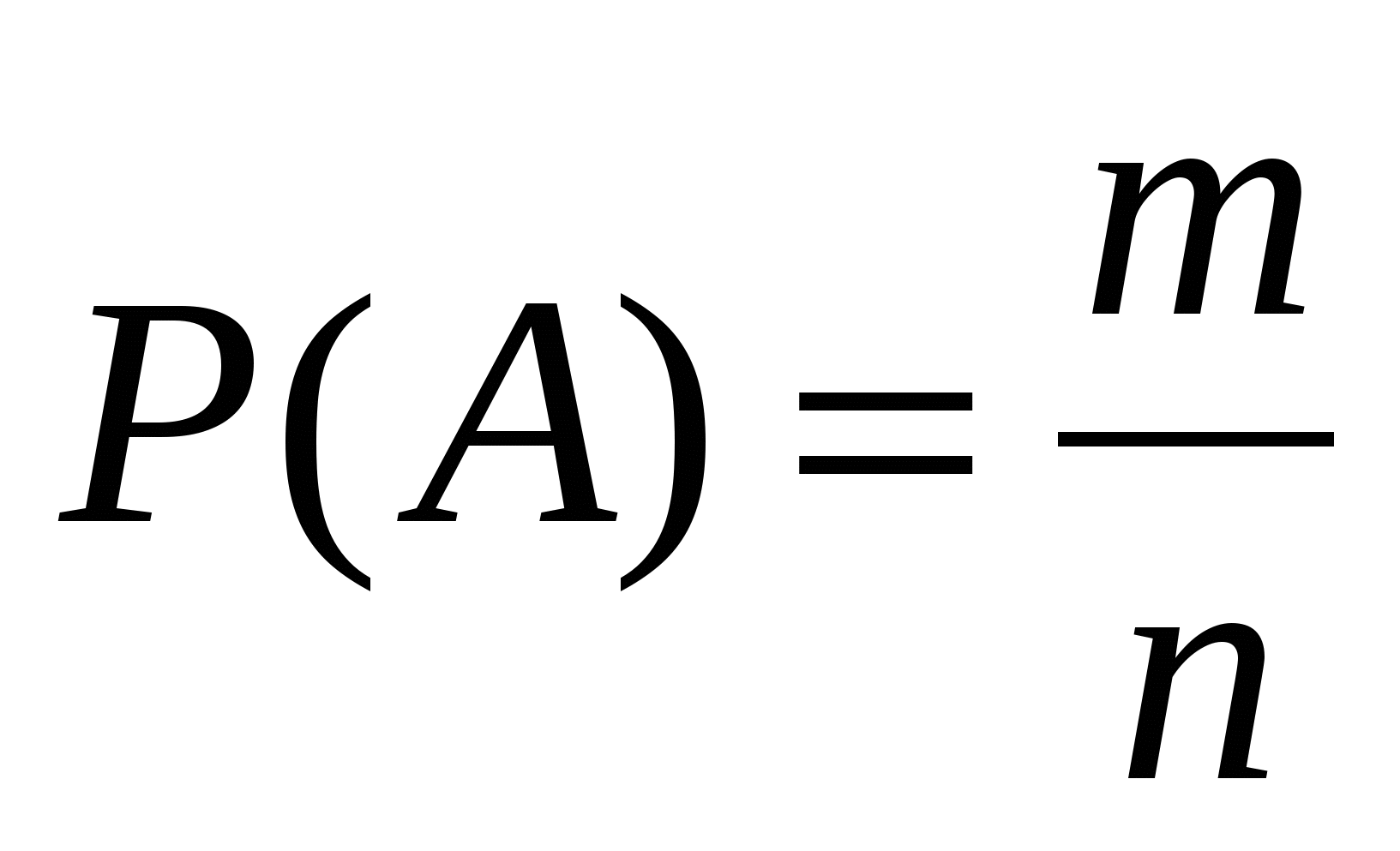, где m - благоприятные исходы, а n - все исходы

События:

Вероятность невозможного события равна 0: Р(А)=0

Вероятность достоверного события равна 1: Р(А)=1

Разберем все события по пунктам 

 Зависимые события:

События называются зависимыми, если одно из них влияет на вероятность появления другого.

Независимые события:

Два события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. Вероятность произведения двух независимых событий A и B равна произведению этих вероятностей:

Р(АВ) = Р(А)Р(В)

Совместные события:

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании. В противном случае события называются несовместными.

Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения:

Р(А+В)=Р(А)+Р(В)−Р(АВ)

Теоремы сложения и умножения вероятностей

Теорема сложения вероятностей: Вероятность суммы двух несовместных событий равно сумме вероятностей этих событий:

Р(А+В) = Р(А)+Р(В)

Теорема умножения вероятностей: Вероятность произведения двух событий равно произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

Р(А * В)= Р(А) * Р(В/А)

Для независимых событий 

Р(А*В)=Р(А)*Р(В)