В5 Простейшие уравнения
 Конспект к уроку "Простейшие уравнения"
Конспект к уроку "Простейшие уравнения"
Простейшие уравнения, представленные в части В, бывают следующих видов:
1. Линейные, квадратные, кубические уравнения
Формулы сокращенного умножения:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
a2 – b2 = (a + b)(a – b)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a - b)3 = a3 - 3a2b + 3ab2 - b3
a3 + b3 = (a + b)( a2 - ab + b2)
a3 – b3 = (a – b)( a2 + ab + b2)
Линейные уравнения имеют свой график – прямая. Причем, от коэффициентов а, b зависит поведение этой прямой
Квадратное уравнение:

График квадратных уравнений представляет собой параболу, ветви которой могут быть направлены вверх (если коэффициент а перед х2 – положительный) или вниз (если коэффициент а перед х2 – отрицательный)
Важно!! Квадратные уравнения можно решать, не находя дискриминант, а пользуясь теоремой Виета:

2. Показательные уравнения
Показательное уравнение — это любое уравнение, содержащее в себе показательную функцию, т.е. выражение вида ах.
Чтобы решать такие уравнения необходимо знать свойства степеней:
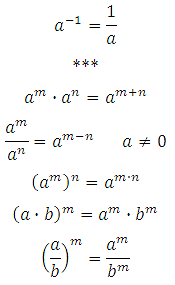
3. Иррациональные уравнения
Иррациональное уравнение — это уравнение, содержащее неизвестное под знаком корня.
Для решения таких уравнений необходимо уметь работать с квадратными корнями:

4. Логарифмические уравнения
Это уравнения, в которых неизвестные переменные находятся внутри логарифмов.
все методы решения логарифмических уравнения роднит одно: их цель свести логарифмические уравнения к простейшему виду:
а затем уже решать уравнение без логарифмов:
f(x) = g(x)
То есть правило такое:
| Если уравнение сведено к такому, что слева и справа от знака «равно» стоят логарифмы с одним основанием, то логарифмы мы «зачеркиваем» и решаем оставшееся уравнение. |
Однако, тут есть один подводный камень: поскольку логарифм
f(x)>0,
то после нахождения корней логарифмического уравнения, мы обязаны сделать проверку!!!
Свойства логарифмов

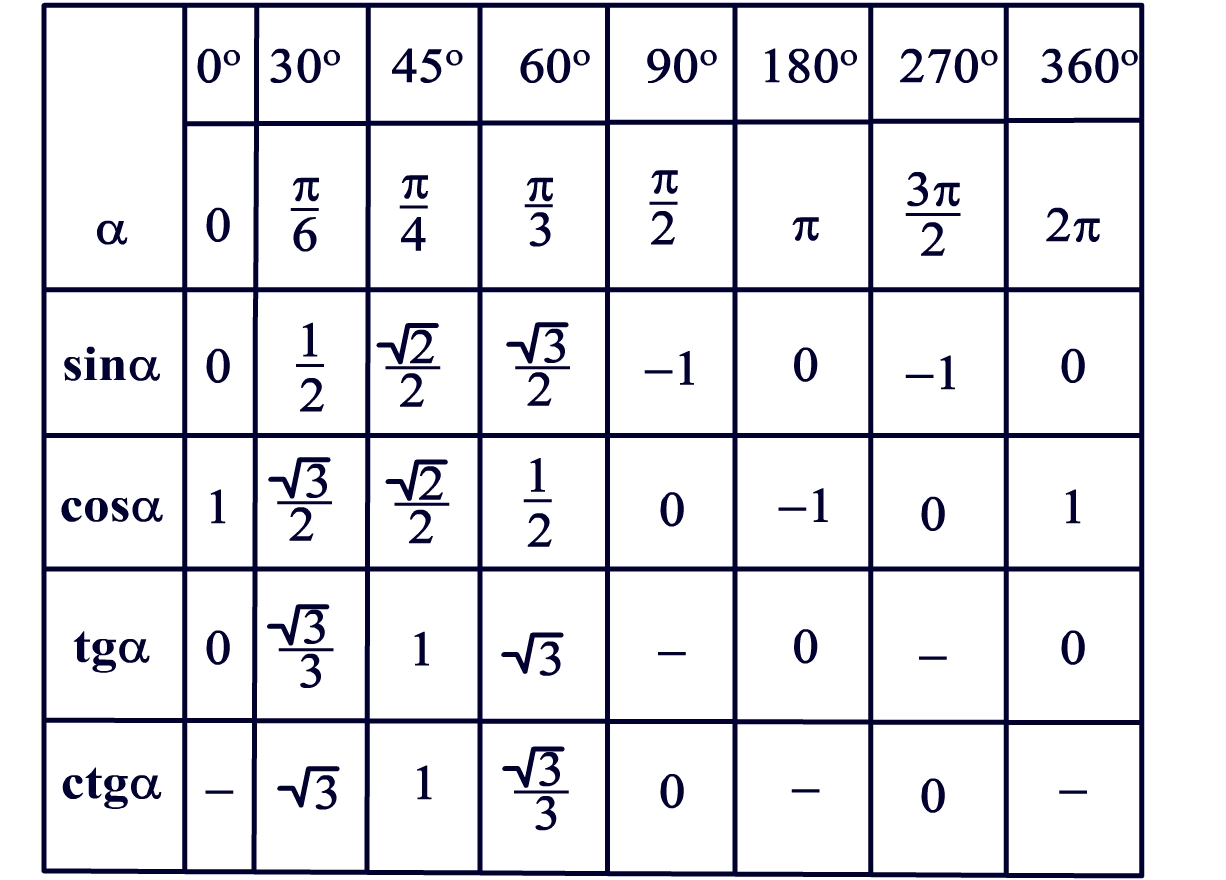
5. Тригонометрические уравнения
Тригонометрические уравнения – уравнения, содержащие переменную под знаком тригонометрических функций.
Для решения таких уравнений необходимо знать, что из себя представляют sin, cos, tg, ctg и знать графики их функций; уметь пользоваться тригонометрическим кругом; знать наизусть таблицу основных углов (0, 30, 45, 60, 90).

Также необходимо вспомнить некоторые свойства тригонометрического круга:
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.